Схема повторных независимых испытаний.

     Рассмотрим опыт, который состоит в том, что испытания повторяются многократно, причем выполнены следующие условия:

     1) все испытания независимы друг от друга, т.е. вероятность появления события А в каждом из них не зависит от того, произошло или не произошло рассматриваемое событие в других опытах;

     2) каждое испытание имеет только два исхода:

     а) событие А произошло; б) событие А не произошло;

     3) вероятность появления события А в каждом испытании постоянна и равна p, а вероятность не появления события А равна q = 1 - p.

     Так как в каждом из n проводимых испытаний событие А может произойти или не произойти, то полученная схема повторных независимых испытаний содержит 2n точек.

     Примерами повторных независимых испытаний с двумя исходами могут служить:

     1) многократное подбрасывание монеты;

     2) стрельба по цели n раз одиночными выстрелами, если нас интересует только попадание или промах;

     3) массовый контроль деталей, при котором требуется только установить, какой является деталь, стандартной или нестандартной.

     Некоторые задачи, описываемые по такой схеме, можно решить, используя формулу для непосредственного подсчета вероятностей или теореме о вероятности суммы и вероятности произведения событий. Однако, проще воспользоваться формулой Бернулли. Пусть необходимо вычислить вероятность появления события А ровно m раз при проведении n повторных независимых испытаний.

     Вероятность появления события А равна p, а вероятность не появления события А равна q, тогда вероятность появления события А ровно m раз при проведении n независимых испытаний равна: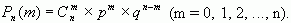

     Эту формулу называют формулой Бернулли.

     Пример. Известно, что при каждом взвешивании равновозможна как положительная, так и отрицательная ошибка. Какова вероятность того, что при пяти взвешиваниях получатся три положительные ошибки?

     Проводится 5 независимых испытаний с двумя исходами, причем в каждом испыта-нии p = q = 0,5. Тогда по формуле Бернулли вероятность появления трех положительных ошибок равна:

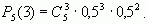
     Cоставим программу для данного примера.

     Надо использовать не только процедуру вычисления числа сочетаний из n элементов по m, но и процедуру вычисления степени заданного вещественного числа a.

{fbern.pas

Сайт Algorithm (http://www.algorithm1.narod.ru/)

Автор проекта: Galina}

var s1 : longint;

p, st, st1 : real;

Procedure combination(n, k : integer; var s : longint);

var i : longint;

begin

  s := 1;

  if k = 0 then s := 1

              else for i := 1 to n - k do s := s*(k + i) div i

end;

Procedure extent(a : real; n : integer; var q : real);

var i : integer;

begin

  q := 1;

  for i := 1 to n do q := a*q

end;

begin

  combination(5, 3, s1);

  extent(0.5, 3, st);

  extent(0.5, 2, st1);

  p := s1*st*st1;

  writeln('Вероятность равна ', p:6:4)

end.