Размещением из n элементов по k называется всякое упорядоченное подмножество данного множества, содержащее k элементов. Другими словами, размещением из n элементов по k называется всякое подмножество данного множества, состоящее из k элементов, которое может отличаться не только элементами, но и порядком их расположения.

     Например, из множества M = {1, 2, 3, 4} можно образовать 12 различных размещений, из 4 по 2:

 

 

     Число размещений, взятых из n элементов по k, мы будем обозначать символом и определять по формуле:

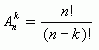
     Значит,

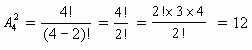
     Вычислить число размещений можно и другим способом:

     Итак,

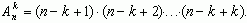
     Таким образом, число размещений из n элементов по k равно произведению k элементов

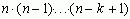
     Например,

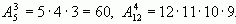
     Таким образом, составив процедуру вычисления размещений по этому принципу, мы избегаем недопустимо больших чисел, которые могут образовываться при вычисление факториалов и упрощаем составление программ, а также имеем возможность в дальнейшем применять процедуру размещений в других программах.

 

     Процедура размещений из n элементов по k элементов

Procedure placement(n, k : integer; var r : longint);

var i : integer;

begin

  r := 1;

  for i := 1 to k do r := r*(n - k + i)

end;

 

     Программа

{placem.pas

Сайт Algorithm (http://www.algorithm1.narod.ru/)

Автор проекта: Galina}

uses Crt;

var n1, k1, r : longint;

{ Процедура вычисления числа размещений из n по k }

Procedure placement(n, k : integer; var r : longint);

var i : integer;

begin

  r := 1;

  for i := 1 to k do r := r*(n - k + i)

end;

begin

  write('Введите n1: ');

  readln(n1);

  write('Введите k1: ');

  readln(k1);

  Placement(n1, k1, r);

  writeln('Число размещений из n1 по k1 равно: ', r)

end.